アフィン変換
変換元の座標を(x,y,z)、変換後の座標を(X,Y,Z)とすると変換計算は以下になります。
X=ax+by+cz+l
Y=dx+ey+fz+m
Z=gx+hy+iz+n
a,b,c,d,e,f,g,h,i,l,m,nの値は指定した変換元と変換先の座標値から計算されます。
変換元と変換先の座標が4点の場合は、変換元の座標を変換した座標と、変換先の座標の差異は0になります。
変換元と変換先の座標が5点以上の場合は、補正された座標になります。
アフィン変換では四角形が歪むような変換が可能になります。(下図は2次元のイメージ)

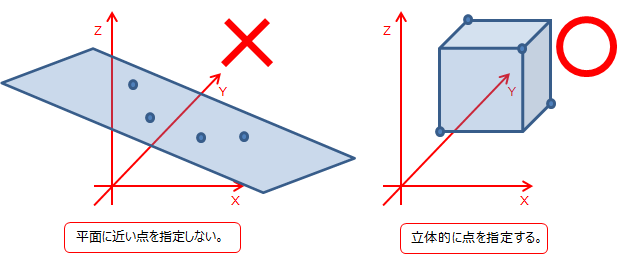
指定した点が平面に近いと変換後の点群も平面に近くなるので、基準点は立体的に指定する必要があります。
(下図参照)