均平精度の算出過程
[ほ場均平度][凹凸計測]それぞれの場合に関して、均平精度の算出過程を説明します。
①指定範囲内の点群の分布状況から基準となる面を作成します。
【ほ場均平度の場合】
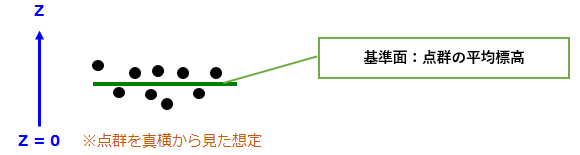
指定範囲内の点群の平均標高位置に基準面を作成します。
【凹凸計測の場合(例:斜面)】
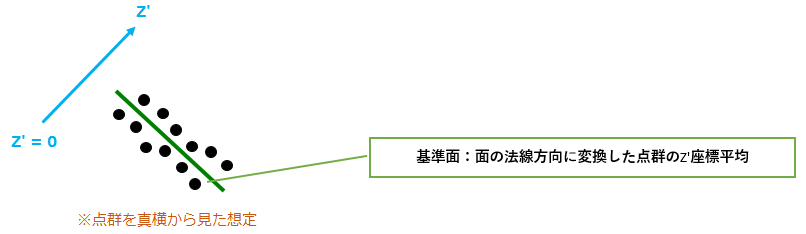
点群から斜面の方向を推定し、その面の法線方向をZ'軸方向とします。
その後、各点群の座標を面の法線方向(Z'軸方向)に変換し、Z'座標の平均位置に基準面を作成します。

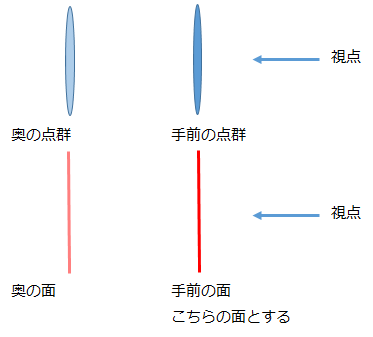
※手前と奥の2つの面がある場合は、手前の面となるように面を決めます。
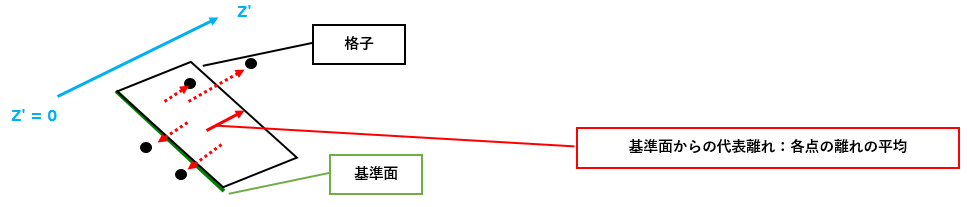
②指定範囲内に格子を配置し、格子単位で基準面との離れを算出します。
【ほ場均平度の場合】

【凹凸計測の場合(例:斜面)】
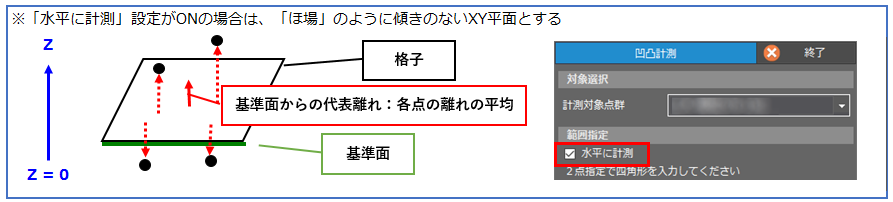
③格子毎の代表離れを集計して計測結果を算出します。
【ほ場均平度の場合】

【凹凸計測の場合(例:斜面)】

メモ
- 標準偏差とは?
「バラつきの大きさを示す値」です。
標準偏差は以下の手順で求めます。
①平均値を求めます。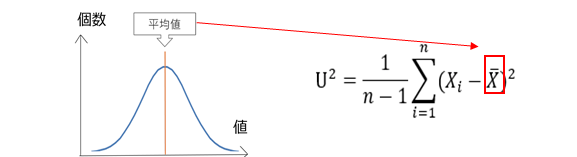
②偏差を求めます。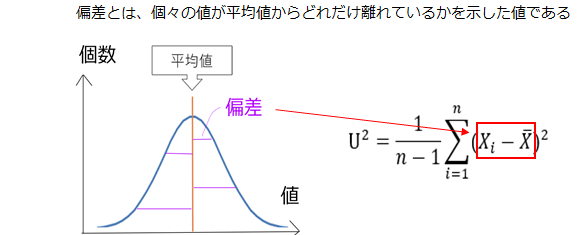
③偏差の平均を求めます。
④標準偏差を求めます。
標準偏差を見ることで、その集団全体のバラつき度合いを知ることができます。
標準偏差が大きいほど、その集団はバラつきが大きいという解釈になります。
- 不偏分散とは?
前提として「母集団」と「標本」に関して説明します。
分散/標準偏差を求める際に、母集団のデータやデータ数を用いると「母分散」、標本のデータやデータ数を用いると「標本分散」が求まります。
「標本分散」は全てのデータを用いて算出しているわけではないので、「母分散」と比べると誤差が出てしまいます。「母分散」に比べると小さい値になってしまいます。(母分散と同等ではないので「不偏性」がないと言われます。)
「標本分散」と「母分散」との誤差を補正して「母分散」と同等の値を得るため「データ数n - 1」で割って分散を求めます。
これで求まった分散の値を「不偏分散」と言います。
※母集団全てのデータを揃えるのは困難なため、統計の分野では、不偏分散が用いられることが多いです。
TREND-POINTの計測に関しても、格子毎の代表値を求め、その代表値の集計で標準偏差を求めているので、補正を行って求める「不偏分散」を用いています。